Zadanie nr 4458038
Wykaż, że dla każdych dwóch różnych liczb rzeczywistych  i
i 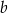 prawdziwa jest nierówność
prawdziwa jest nierówność
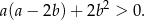
Rozwiązanie
Przekształcamy daną nierówność w sposób równoważny
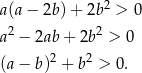
Teraz jest jasne, że nierówność ta jest zawsze spełniona (bo 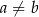 ).
).
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla każdych dwóch różnych liczb rzeczywistych  i
i 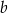 prawdziwa jest nierówność
prawdziwa jest nierówność
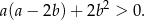
Przekształcamy daną nierówność w sposób równoważny
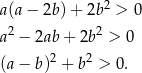
Teraz jest jasne, że nierówność ta jest zawsze spełniona (bo 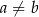 ).
).
