Zadanie nr 4628017
Udowodnij, że dla dowolnych liczb rzeczywistych 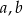 prawdziwa jest nierówność
prawdziwa jest nierówność
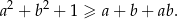
Rozwiązanie
Sposób I
Przekształcamy daną nierówność w sposób równoważny.
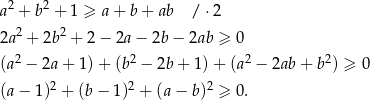
Otrzymana nierówność jest oczywiście prawdziwa, więc wyjściowa nierówność też musiała być spełniona.
Sposób II
Potraktujmy daną nierówność
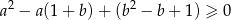
Jako zwykłą nierówność kwadratową zmiennej  . Liczymy
. Liczymy 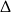 -ę.
-ę.
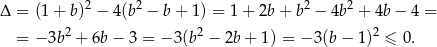
Ponieważ 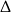 jest zawsze niedodatnia, wykres trójmianu będącego lewą stroną nierówności nie schodzi poniżej osi
jest zawsze niedodatnia, wykres trójmianu będącego lewą stroną nierówności nie schodzi poniżej osi 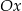 (może być styczny do osi
(może być styczny do osi 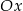 ). Zatem rzeczywiście
). Zatem rzeczywiście