Zadanie nr 6032703
Udowodnij, że dla dowolnych liczb rzeczywistych 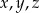 takich, że
takich, że 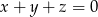 , prawdziwa jest nierówność
, prawdziwa jest nierówność 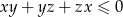 .
.
Możesz skorzystać z tożsamości 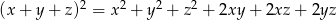 .
.
Rozwiązanie
Sposób I
Korzystając z podanej tożsamości mamy
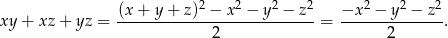
Otrzymane wyrażenie jest oczywiście zawsze niedodatnie.
Sposób II
Zauważmy najpierw, że przynajmniej dwie z liczb 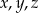 mają różne znaki (lub są równe 0). Bez zmniejszania ogólności możemy założyć, że tę własność mają liczby
mają różne znaki (lub są równe 0). Bez zmniejszania ogólności możemy założyć, że tę własność mają liczby  i
i 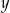 , tzn.
, tzn. 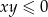 . Korzystając z warunku
. Korzystając z warunku 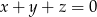 będziemy przekształcać lewą stronę nierówności.
będziemy przekształcać lewą stronę nierówności.
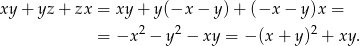
Zauważmy teraz, że na mocy założenia 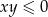 otrzymane wyrażenie jest zawsze niedodatnie.
otrzymane wyrażenie jest zawsze niedodatnie.

