Zadanie nr 6816166
Wykaż, że jeżeli 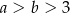 , to
, to 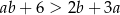 .
.
Rozwiązanie
Przekształćmy daną nierówność w sposób równoważny.
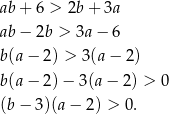
Widać teraz, że przy danym założeniu: 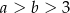 , wyrażenia w obu nawiasach są dodatnie.
, wyrażenia w obu nawiasach są dodatnie.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli 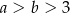 , to
, to 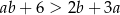 .
.
Przekształćmy daną nierówność w sposób równoważny.
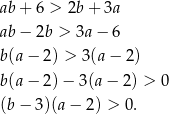
Widać teraz, że przy danym założeniu: 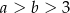 , wyrażenia w obu nawiasach są dodatnie.
, wyrażenia w obu nawiasach są dodatnie.
