/Szkoła średnia/Nierówności/Udowodnij.../Kwadratowe

Zadanie nr 8214214

Dodaj do ulubionych
Dodaj do rozwiązanych

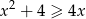Wykaż, że dla każdej liczby rzeczywistej x prawdziwa jest nierówność x 2 + 4 ≥ 4x .

Rozwiązanie

Dana nierówność to zwykła nierówność kwadratowa

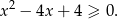
2 x − 4x + 4 ≥ 0.

Sposób I

Lewa strona nierówności to pełen kwadrat, więc możemy ją zapisać w postaci

2 (x − 2) ≥ 0.

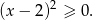
Teraz jest jasne, że nierówność ta jest zawsze spełniona.

Sposób II

Liczmy 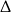Δ -ę.

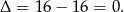
Δ = 16 − 16 = 0.

To oznacza, że wykresem lewej strony jest parabola o ramionach skierowanych w górę, która jest styczna do osi 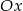Ox . To oznacza, że lewa strona nie przyjmuje wartości ujemnych, czyli rzeczywiście

x2 − 4x + 4 ≥ 0.
Wersja PDF