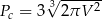/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema

Zadanie nr 2035964

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozważamy wszystkie walce o objętości 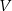V . Wyznacz wysokość i promień podstawy tego z rozważanych walców, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to pole.

Rozwiązanie

Szkicujemy walec – oznaczmy jego wysokość i promień podstawy przez 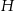H i r odpowiednio.

PIC

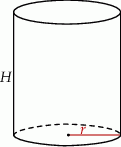
Z podanej objętości mamy

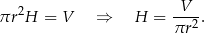
πr2H = V ⇒ H = -V--. πr2

Obliczamy pole powierzchni całkowitej walca.

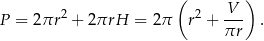
( V ) P = 2 πr2 + 2πrH = 2π r2 + --- . πr

Musimy zatem wyznaczyć wartość najmniejszą funkcji 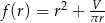V f (r) = r2 + πr na przedziale 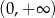(0 ,+∞ ) . Liczymy pochodną

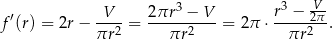
′ -V-- 2-πr3-−-V- r3 −-V2π- f (r) = 2r − πr 2 = πr 2 = 2π ⋅ πr2 .

Widzimy zatem, że na przedziale 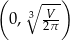( ∘ --) 3 V-- 0, 2π pochodna jest ujemna, czyli 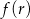f (r) maleje, a w przedziale 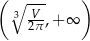(∘ --- ) 3 V2π,+ ∞ pochodna jest dodatnia, czyli 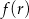f(r) rośnie. Zatem najmniejszą możliwą wartość 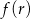f(r) otrzymamy dla 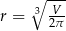∘ --- r = 3 -V- 2π . Wtedy

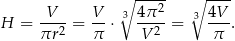
∘ ---2- ∘ ---- H = -V-- = V- ⋅ 3 4π--= 3 4V- . πr 2 π V 2 π

Pole powierzchni całkowitej jest wtedy równe

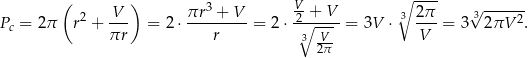
( ) 3 V- ∘ ---- √ ------ Pc = 2π r2 + V-- = 2 ⋅ πr-+--V-= 2 ⋅2∘+--V-= 3V ⋅ 3 2π- = 3 32πV 2. πr r 3 -V- V 2π

 
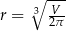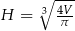Odpowiedź: ∘ --- 3 V-- r = 2π , ∘ --- 3 4V- H = π , √ ------ Pc = 3 3 2πV 2

Wersja PDF