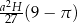Zadanie nr 2185517
W metalowym ostrosłupie prawidłowym czworokątnym o wysokości 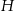 i krawędzi podstawy
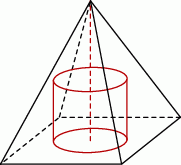
i krawędzi podstawy  wydrążono otwór w kształcie walca, którego oś symetrii pokrywa się z osią symetrii ostrosłupa (patrz rysunek). Otwór wydrążono przez podstawę ostrosłupa w ten sposób, że górna podstawa walca nie wystaje poza powierzchnię ostrosłupa. Jaka może być najmniejsza możliwa objętość otrzymanej w ten sposób bryły?
wydrążono otwór w kształcie walca, którego oś symetrii pokrywa się z osią symetrii ostrosłupa (patrz rysunek). Otwór wydrążono przez podstawę ostrosłupa w ten sposób, że górna podstawa walca nie wystaje poza powierzchnię ostrosłupa. Jaka może być najmniejsza możliwa objętość otrzymanej w ten sposób bryły?
Rozwiązanie
Objętość otrzymanej bryły będzie najmniejsza, gdy objętość wydrążonego walca będzie największa. W szczególności górna podstawa walca musi być styczna do ścian bocznych ostrosłupa. Naszkicujmy przekrój opisanej sytuacji płaszczyzną przechodzącą przez oś symetrii ostrosłupa i prostopadłą do jednej z krawędzi podstawy.
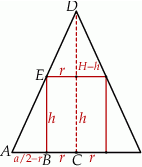
Jeżeli  jest promieniem podstawy walca, a
jest promieniem podstawy walca, a 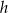 jego wysokością, to z podobieństwa trójkątów
jego wysokością, to z podobieństwa trójkątów 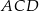 i
i 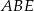 mamy
mamy
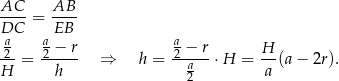
Objętość walca jest więc równa
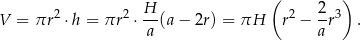
Sprawdzamy teraz kiedy funkcja
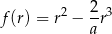
określona dla 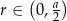 przyjmuje wartość największą. Liczymy pochodną
przyjmuje wartość największą. Liczymy pochodną
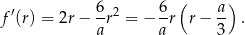
Widać stąd, że na przedziale 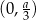 funkcja jest rosnąca (pochodna jest dodatnia), a na przedziale
funkcja jest rosnąca (pochodna jest dodatnia), a na przedziale 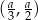 malejąca (pochodna jest ujemna). Zatem największą objętość walca otrzymamy dla
malejąca (pochodna jest ujemna). Zatem największą objętość walca otrzymamy dla 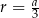 . Jest ona wtedy równa
. Jest ona wtedy równa
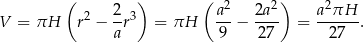
Obliczamy jeszcze objętość bryły otrzymanej z ostrosłupa przez wycięcie walca.
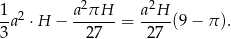
Odpowiedź: