Zadanie nr 2870137
Trójkąt równoramienny o obwodzie 12 obraca się wokół swojej osi symetrii. Oblicz dla jakich długości boków trójkąta otrzymamy stożek, w którym różnica między polem powierzchni bocznej, a polem podstawy jest największa. Oblicz objętość tego stożka.
Rozwiązanie
Jeżeli oznaczmy długość ramienia trójkąta przez  , to podstawa ma długość
, to podstawa ma długość 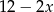 i wyniku obrotu otrzymamy stożek o promieniu podstawy
i wyniku obrotu otrzymamy stożek o promieniu podstawy 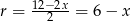 i tworzącej długości
i tworzącej długości 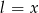 .
.
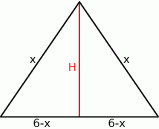
Zauważmy jeszcze, że musi być 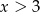 (żeby ramię było dłuższe od połowy podstawy) oraz
(żeby ramię było dłuższe od połowy podstawy) oraz 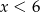 .
.
Różnica między polem powierzchni bocznej, a polem podstawy otrzymanego stożka jest równa
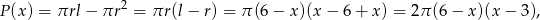
gdzie 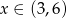 . Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w dół. Jej wierzchołek znajduje się dokładnie między pierwiastki, czyli największą różnicę pól otrzymamy dla
. Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w dół. Jej wierzchołek znajduje się dokładnie między pierwiastki, czyli największą różnicę pól otrzymamy dla 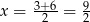 , czyli dla
, czyli dla 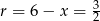 .
.
Pozostało obliczyć objętość stożka. Jego wysokość jest równa
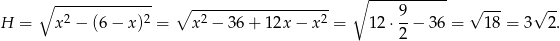
Liczymy objętość.
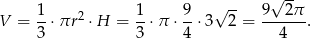
Odpowiedź: Boki trójkąta: 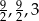 , objętość:
, objętość: 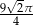 .
.

