Zadanie nr 3682797
Romb o boku długości  obraca się dokoła jednej z przekątnych. Wyznacz pole tego spośród takich rombów, dla którego objętość otrzymanej bryły jest największa.
obraca się dokoła jednej z przekątnych. Wyznacz pole tego spośród takich rombów, dla którego objętość otrzymanej bryły jest największa.
Rozwiązanie
Szkicujemy bryłę, którą otrzymamy obracając romb.
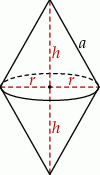
Widać, że są to dwa stożki sklejone podstawami. Jeżeli oznaczymy promień podstawy utworzonych stożków przez  , a ich wysokość przez
, a ich wysokość przez 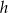 , to mamy
, to mamy
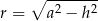
i objętość otrzymanej bryły jest równa
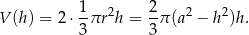
Wyznaczenie bryły o największej objętości sprowadza się więc do wyznaczenia największej wartości funkcji
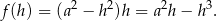
Liczymy pochodną tej funkcji
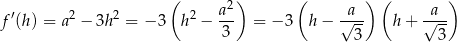
Dziedziną funkcji 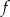 jest przedział
jest przedział 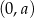 i w tym przedziale pochodna ma jedno miejsce zerowe
i w tym przedziale pochodna ma jedno miejsce zerowe 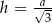 . Ponadto na lewo od tego miejsca zerowego pochodna jest dodatnia, a na prawo jest ujemna. To oznacza, że funkcja
. Ponadto na lewo od tego miejsca zerowego pochodna jest dodatnia, a na prawo jest ujemna. To oznacza, że funkcja 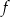 rośnie w przedziale
rośnie w przedziale 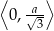 i maleje w przedziale
i maleje w przedziale 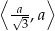 . W takim razie największą objętość bryły otrzymamy dla
. W takim razie największą objętość bryły otrzymamy dla 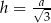 . Wtedy
. Wtedy
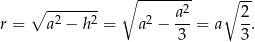
Pole powierzchni rombu dla którego otrzymujemy tę maksymalną objętość jest równe (korzystamy ze wzoru na pole rombu z przekątnymi)
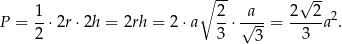
Odpowiedź: