Zadanie nr 5404267
Objętość graniastosłupa prawidłowego czworokątnego jest równa 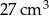 , Pole powierzchni całkowitej graniastosłupa jest funkcją długości jego krawędzi podstawy. Napisz wzór tej funkcji i wyznacz jej przedziały monotoniczności.
, Pole powierzchni całkowitej graniastosłupa jest funkcją długości jego krawędzi podstawy. Napisz wzór tej funkcji i wyznacz jej przedziały monotoniczności.
Rozwiązanie
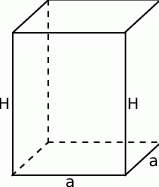
Jeżeli oznaczymy długość krawędzi podstawy graniastosłupa przez  , a jego wysokość przez
, a jego wysokość przez 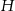 to mamy równanie
to mamy równanie
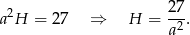
Liczymy teraz pole powierzchni całkowitej
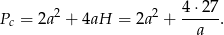
Oznaczmy to wyrażenie przez 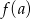 . Aby wyznaczyć przedziały monotoniczności funkcji
. Aby wyznaczyć przedziały monotoniczności funkcji 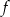 , liczymy jej pochodną
, liczymy jej pochodną
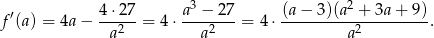
Ponieważ 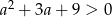 mamy
mamy 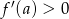 dla
dla 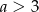 i
i 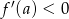 dla
dla 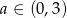 . Zatem funkcja
. Zatem funkcja 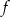 jest na tych przedziałach odpowiednio rosnąca i malejąca.
jest na tych przedziałach odpowiednio rosnąca i malejąca.
Odpowiedź: 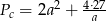 , rosnąca dla
, rosnąca dla 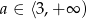 , malejąca dla
, malejąca dla