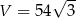Zadanie nr 5953809
W stożek o promieniu podstawy 6 i wysokości 8 wpisujemy graniastosłupy prawidłowe sześciokątne tak, że jedna podstawa jest zawarta w podstawie stożka, a pozostałe wierzchołki należą do powierzchni bocznej stożka. Oblicz objętość graniastosłupa o największym polu powierzchni bocznej.
Rozwiązanie
Gdy narysujemy rysunek staje się jasne, że wystarczy rozważać przekrój 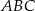 .
.
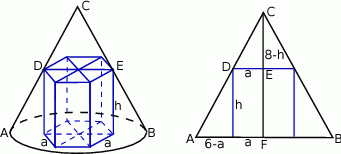
Z podobieństwa trójkątów 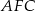 i
i 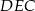 mamy
mamy
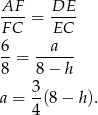
Stąd pole powierzchni bocznej graniastosłupa
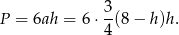
Jako funkcja zmiennej 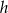 jest to parabola o ramionach skierowanych w dół, więc wartość największą osiąga w wierzchołku, czyli dla
jest to parabola o ramionach skierowanych w dół, więc wartość największą osiąga w wierzchołku, czyli dla 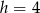 (dokładnie w środku między pierwiastkami). Wtedy
(dokładnie w środku między pierwiastkami). Wtedy
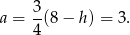
Pozostało policzyć objętość graniastosłupa (korzystamy ze wzoru na pole trójkąta równobocznego).
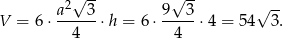
Odpowiedź: