Zadanie nr 6014766
Rozważmy wszystkie graniastosłupy prawidłowe trójkątne o objętości 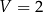 . Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
. Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
Rozwiązanie
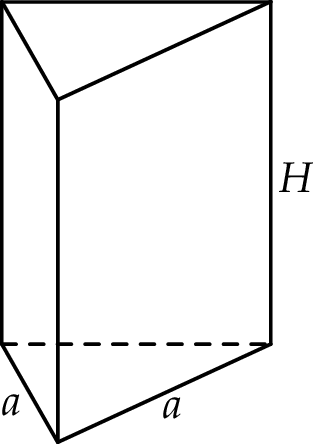
Oznaczmy przez  długość krawędzi podstawy, a przez
długość krawędzi podstawy, a przez 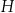 wysokość graniastosłupa.
wysokość graniastosłupa.
Z podanej objętości mamy
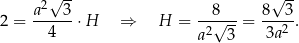
Liczymy teraz pole powierzchni całkowitej.
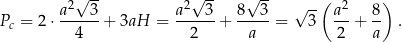
Aby otrzymać najmniejsze pole całkowite musimy więc wyznaczyć najmniejszą możliwą wartość funkcji 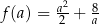 określonej dla
określonej dla 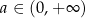 . Liczymy pochodną
. Liczymy pochodną
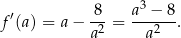
Widać teraz, że pochodna jest ujemna dla 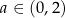 i dodatnia dla
i dodatnia dla 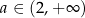 . To oznacza, że funkcja
. To oznacza, że funkcja 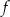 jest malejąca w przedziale
jest malejąca w przedziale 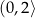 i rosnąca w przedziale
i rosnąca w przedziale 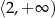 . Najmniejsze pole otrzymamy więc dla
. Najmniejsze pole otrzymamy więc dla 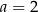 . Wysokość prostopadłościanu jest wtedy równa
. Wysokość prostopadłościanu jest wtedy równa
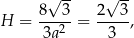
a jego pole powierzchni całkowitej jest równe
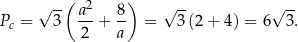
Odpowiedź: 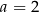 ,
, 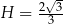 ,
, 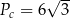 .
.

