/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema

Zadanie nr 7901084

Dodaj do ulubionych
Dodaj do rozwiązanych

Tekturowy karton ma mieć kształt prostopadłościanu, którego podstawa jest prostokątem o jednym z boków dłuższym od drugiego o 24 cm. Suma wszystkich krawędzi tego prostopadłościanu ma być równa 480 cm.

  • Napisz wzór funkcji 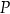P wyrażającej całkowite pole zewnętrznej powierzchni kartonu, w zależności od długości x krótszej krawędzi jego podstawy. Podaj dziedzinę funkcji P .

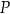  • Oblicz jakie powinny być wymiary tego kartonu tak, aby łączne pole powierzchni jego ścian było największe możliwe.

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.