Zadanie nr 8124674
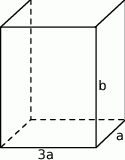
Rozpatrujemy wszystkie prostopadłościany o objętości 27, których stosunek długości dwóch krawędzi wychodzących z tego samego wierzchołka jest równy 1:3 oraz suma długości wszystkich dwunastu krawędzi jest mniejsza od 52. Wyznacz pole powierzchni całkowitej prostopadłościanu jako funkcję długości jednej z jego krawędzi. Wyznacz dziedzinę tej funkcji. Oblicz wymiary tego spośród rozpatrywanych prostopadłościanów, którego pole powierzchni całkowitej jest najmniejsze.
Rozwiązanie
Oznaczmy przez 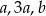 długości krawędzi prostopadłościanu.
długości krawędzi prostopadłościanu.
Z podanej objętości mamy
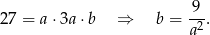
Zapiszmy jeszcze warunek z sumą długości wszystkich krawędzi mniejszą od 52.
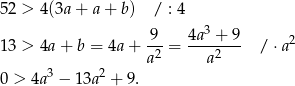
Aby rozwiązać tę nierówność musimy najpierw rozłożyć prawą stronę na czynniki. Łatwo zauważyć, że jednym z pierwiastków prawej strony jest 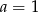 . Dzielimy więc ten wielomian przez
. Dzielimy więc ten wielomian przez 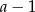 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
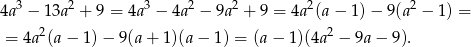
Rozkładamy jeszcze trójmian w nawiasie.
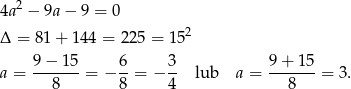
Mamy zatem nierówność
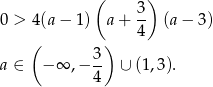
Ponieważ interesują nas tylko dodatnie wartości  , mamy stąd
, mamy stąd 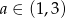 .
.
Liczymy teraz pole powierzchni całkowitej prostopadłościanu.
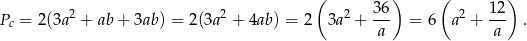
Dziedziną tej funkcji jest przedział 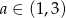 .
.
Aby otrzymać najmniejsze pole całkowite musimy więc wyznaczyć najmniejszą możliwą wartość funkcji 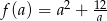 określonej dla
określonej dla 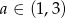 . Liczymy pochodną
. Liczymy pochodną
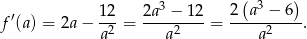
Widać teraz, że pochodna jest ujemna dla 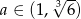 i dodatnia dla
i dodatnia dla 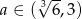 . To oznacza, że funkcja
. To oznacza, że funkcja 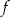 jest malejąca w przedziale
jest malejąca w przedziale 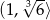 i rosnąca w przedziale
i rosnąca w przedziale 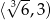 . Najmniejsze pole otrzymamy więc dla
. Najmniejsze pole otrzymamy więc dla 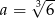 . Pozostałe krawędzie prostopadłościanu mają wtedy długości
. Pozostałe krawędzie prostopadłościanu mają wtedy długości 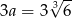 i
i
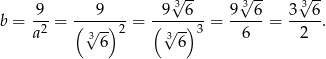
Odpowiedź: 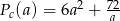 dla
dla 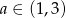 , długości krawędzi:
, długości krawędzi: 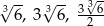 .
.

