Zadanie nr 8386531
W ostrosłup prawidłowy czworokątny o wysokości 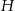 wpisano sześcian tak, że cztery jego wierzchołki należą do krawędzi bocznych ostrosłupa, a cztery pozostałe należą do płaszczyzny jego podstawy. Oblicz dla jakiej długości krawędzi podstawy ostrosłupa stosunek objętości ostrosłupa do objętości sześcianu jest najmniejszy możliwy.
wpisano sześcian tak, że cztery jego wierzchołki należą do krawędzi bocznych ostrosłupa, a cztery pozostałe należą do płaszczyzny jego podstawy. Oblicz dla jakiej długości krawędzi podstawy ostrosłupa stosunek objętości ostrosłupa do objętości sześcianu jest najmniejszy możliwy.
Rozwiązanie
Szkicujemy opisaną sytuację.
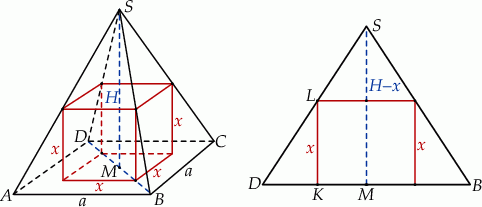
Oznaczmy przez  długość krawędzi podstawy ostrosłupa, a przez
długość krawędzi podstawy ostrosłupa, a przez  długość krawędzi sześcianu. Patrzymy teraz na przekrój ostrosłupa płaszczyzną
długość krawędzi sześcianu. Patrzymy teraz na przekrój ostrosłupa płaszczyzną 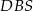 i korzystamy z podobieństwa trójkątów
i korzystamy z podobieństwa trójkątów 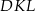 i
i 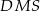 .
.
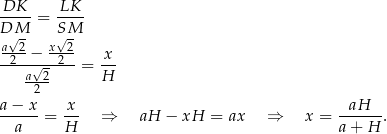
Stosunek objętości ostrosłupa do objętości sześcianu jest więc równy
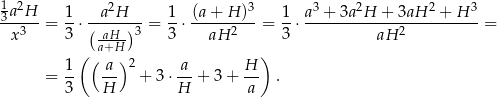
Widać teraz, że możemy podstawić 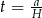 – dzięki temu mamy jedną literkę, a nie dwie. Wystarczy teraz wyznaczyć najmniejszą możliwą wartość funkcji
– dzięki temu mamy jedną literkę, a nie dwie. Wystarczy teraz wyznaczyć najmniejszą możliwą wartość funkcji
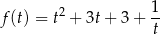
określonej dla 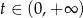 . Liczymy pochodną
. Liczymy pochodną
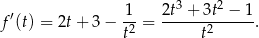
Szukamy miejsc zerowych licznika – jednym z nich jest 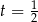 . Dzielimy teraz wielomian w liczniku przez
. Dzielimy teraz wielomian w liczniku przez 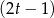 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
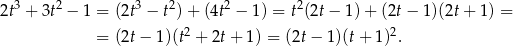
To oznacza, że pochodna jest ujemna dla 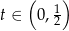 i nieujemna dla
i nieujemna dla 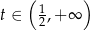 . W takim razie funkcja
. W takim razie funkcja 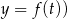 w
w 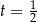 osiąga minimum globalne. Mamy wtedy
osiąga minimum globalne. Mamy wtedy
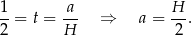
Odpowiedź: