Zadanie nr 1799088
Częścią wspólną płaszczyzny 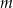 i kuli
i kuli 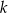 o środku
o środku 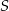 i promieniu
i promieniu 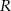 jest koło
jest koło  . Jaka musi być odległość płaszczyzny
. Jaka musi być odległość płaszczyzny 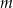 od środka kuli
od środka kuli 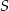 , aby stożek o podstawie
, aby stożek o podstawie  i wierzchołku
i wierzchołku 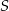 miał największą możliwą objętość? Oblicz tę maksymalną objętość.
miał największą możliwą objętość? Oblicz tę maksymalną objętość.
Rozwiązanie
Rysujemy przekrój osiowy opisanej sytuacji.
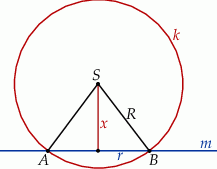
Jeżeli oznaczymy przez  odległość płaszczyzny
odległość płaszczyzny 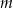 od środka kuli, a przez
od środka kuli, a przez  promień podstawy stożka, to
promień podstawy stożka, to
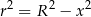
i objętość stożka jest równa
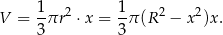
Musimy zatem wyznaczyć największą możliwą wartość funkcji
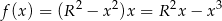
określonej na przedziale 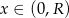 . Liczymy pochodną
. Liczymy pochodną
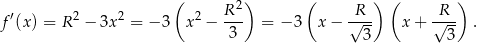
Wykresem pochodnej jest parabola o ramionach skierowanych w dół, zatem w przedziale 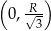 pochodna jest dodatnia, czyli
pochodna jest dodatnia, czyli 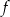 rośnie, a w przedziale
rośnie, a w przedziale 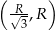 pochodna jest ujemna, czyli funkcja maleje. Największa wartość jest więc przyjmowana dla
pochodna jest ujemna, czyli funkcja maleje. Największa wartość jest więc przyjmowana dla 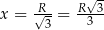 . Mamy wtedy
. Mamy wtedy
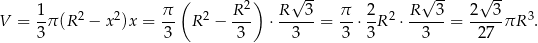
Odpowiedź: Odległość: 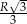 , objętość:
, objętość: 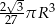 .
.

