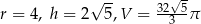Zadanie nr 2007335
Rozpatrujemy wszystkie stożki, których przekrojem osiowym jest trójkąt o obwodzie 20. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.
Rozwiązanie
Szkicujemy stożek
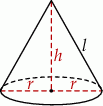
Jeżeli za parametr przyjmiemy promień podstawy  stożka, to mamy
stożka, to mamy
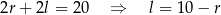
oraz
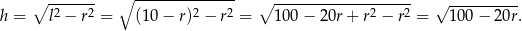
Objętość stożka jest więc równa
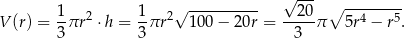
Wyznaczenie największej wartości objętości sprowadza się więc do wyznaczenia największej wartości funkcji
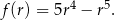
Dziedziną tej funkcji jest przedział 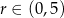 (bo musi być
(bo musi być 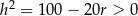 ). Liczymy pochodną
). Liczymy pochodną
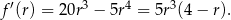
Widać teraz, że pochodna jest dodatnia w przedziale 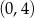 i ujemna w przedziale
i ujemna w przedziale 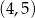 . To oznacza, że funkcja
. To oznacza, że funkcja 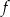 rośnie w przedziale
rośnie w przedziale 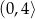 i maleje w przedziale
i maleje w przedziale 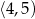 . W takim razie największą wartość objętość otrzymamy dla
. W takim razie największą wartość objętość otrzymamy dla 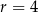 .
.
Wysokość dla 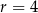 jest równa
jest równa
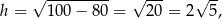
a objętość wynosi
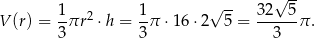
Odpowiedź: