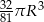Zadanie nr 4345491
W kulę o promieniu długości 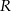 wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.
wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.
Rozwiązanie
Rysujemy przekrój osiowy opisanej sytuacji.
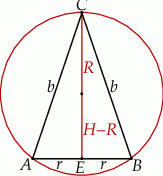
Oznaczmy wysokość i promień podstawy stożka przez  i
i  odpowiednio. Mamy wtedy
odpowiednio. Mamy wtedy
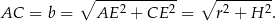
Spróbujemy teraz obliczyć promień podstawy stożka  w zależności od
w zależności od 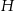 i
i 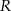 . W tym celu korzystamy ze wzoru
. W tym celu korzystamy ze wzoru 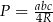 trójkąta (inny sposób to skorzystać z twierdzenia sinusów:
trójkąta (inny sposób to skorzystać z twierdzenia sinusów: 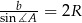 ).
).
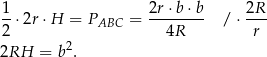
Mamy zatem

Objętość stożka jest więc równa
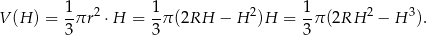
Wyrażenie to ma sens jeżeli 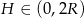 . Aby ustalić dla jakiej wartości
. Aby ustalić dla jakiej wartości 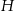 objętość stożka jest największa obliczamy pochodną tej funkcji.
objętość stożka jest największa obliczamy pochodną tej funkcji.
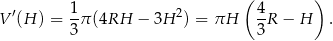
Ponieważ pochodna jest dodatnia w przedziale 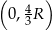 i ujemna w przedziale
i ujemna w przedziale 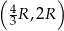 , funkcja
, funkcja 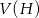 rośnie w pierwszym z tych przedziałów, a maleje w drugim. To oznacza, że największą wartość tej funkcji otrzymamy dla
rośnie w pierwszym z tych przedziałów, a maleje w drugim. To oznacza, że największą wartość tej funkcji otrzymamy dla 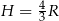 . Objętość jest wtedy równa
. Objętość jest wtedy równa
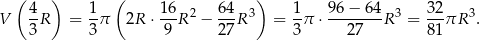
Odpowiedź: