Zadanie nr 4563286
Z kawałka blachy w kształcie sześciokąta foremnego o boku długości 60 cm robimy pudełko o sześciokątnym dnie (otwarte od góry) w następujący sposób: przy każdym wierzchołku odcinamy taki sam deltoid, tnąc w tej samej odległości od wierzchołka raz prostopadle do jednego, a drugi raz do drugiego boku, następnie zaginamy blachę wzdłuż przerywanych linii i lutujemy krawędzie (zobacz rysunek).
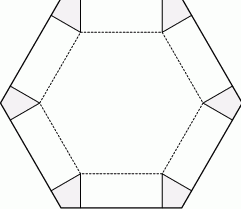
Oblicz długość krawędzi podstawy tego pudełka, którego objętość jest największa. Oblicz tę objętość.
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

