Zadanie nr 4588495
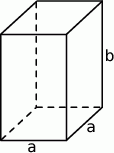
Rozpatrujemy wszystkie graniastosłupy prawidłowe czworokątne, których pole powierzchni całkowitej jest równe 2. Oblicz długości krawędzi tego graniastosłupa, który ma największą objętość. Podaj tę największą objętość.
Rozwiązanie
Oznaczmy przez  długość krawędzi podstawy prostopadłościanu, a przez
długość krawędzi podstawy prostopadłościanu, a przez 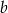 długość jego wysokości.
długość jego wysokości.
Z podanego pola powierzchni całkowitej mamy
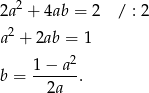
Liczymy teraz objętość prostopadłościanu.
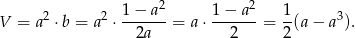
Aby otrzymać największą objętość prostopadłościanu musimy więc wyznaczyć największą możliwą wartość funkcji 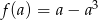 określonej dla
określonej dla 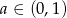 (
(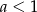 , bo musi być
, bo musi być 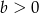 ). Liczymy pochodną
). Liczymy pochodną
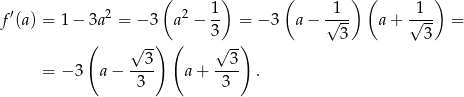
Widać teraz, że pochodna jest dodatnia dla 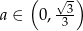 i ujemna dla
i ujemna dla 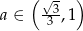 . To oznacza, że funkcja
. To oznacza, że funkcja 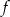 jest rosnąca w przedziale
jest rosnąca w przedziale 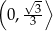 i malejąca w przedziale
i malejąca w przedziale 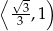 . Największą wartość objętości otrzymamy więc dla
. Największą wartość objętości otrzymamy więc dla 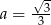 . Wysokość graniastosłupa jest wtedy równa
. Wysokość graniastosłupa jest wtedy równa
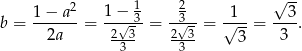
To oznacza, że otrzymany graniastosłup jest sześcianem i jego objętość jest równa
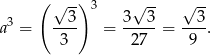
Odpowiedź: Długości krawędzi: 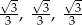 , objętość:
, objętość: 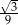 .
.

