Zadanie nr 4686427
Podstawą prostopadłościanu jest prostokąt, w którym jeden bok jest dwa razy dłuższy od drugiego. Pole powierzchni całkowitej tego prostopadłościanu jest równe 1. Jakie powinny być wymiary tego prostopadłościanu, aby jego objętość była największa? Oblicz tę największą objętość.
Rozwiązanie
Oznaczmy przez  i
i 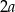 długości krawędzi podstawy prostopadłościanu, a przez
długości krawędzi podstawy prostopadłościanu, a przez 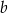 długość jego wysokości.
długość jego wysokości.
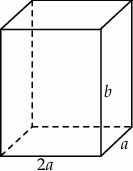
Z podanego pola powierzchni całkowitej mamy
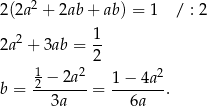
Liczymy teraz objętość prostopadłościanu.
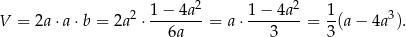
Aby otrzymać największą objętość prostopadłościanu musimy więc wyznaczyć największą możliwą wartość funkcji 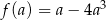 określonej dla
określonej dla 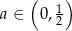 (
(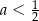 , bo musi być
, bo musi być 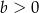 ). Liczymy pochodną
). Liczymy pochodną
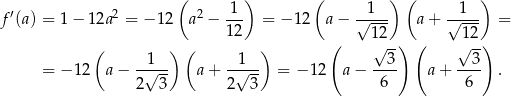
Widać teraz, że pochodna jest dodatnia dla 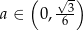 i ujemna dla
i ujemna dla 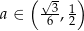 . To oznacza, że funkcja
. To oznacza, że funkcja 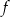 jest rosnąca w przedziale
jest rosnąca w przedziale 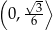 i malejąca w przedziale
i malejąca w przedziale 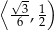 . Największą wartość objętości otrzymamy więc dla
. Największą wartość objętości otrzymamy więc dla 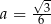 . Pozostałe krawędzie prostopadłościanu mają wtedy długości
. Pozostałe krawędzie prostopadłościanu mają wtedy długości 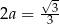 i
i
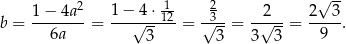
Objętość dla tych długości krawędzi jest równa
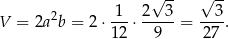
Odpowiedź: Długości krawędzi: 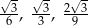 , objętość:
, objętość: 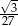 .
.

