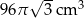/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema/Największa objętość

Zadanie nr 4768500

Dodaj do ulubionych
Dodaj do rozwiązanych

Jaką największą objętość ma walec wpisany w kulę o średnicy długości 12 cm?

Rozwiązanie

Rysujemy przekrój osiowy opisanej sytuacji.

PIC

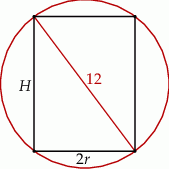
Liczymy objętość walca.

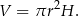
V = πr 2H .

Mamy ponadto

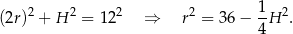
1 (2r)2 + H 2 = 122 ⇒ r2 = 36 − --H 2. 4

Podstawiamy to do wzoru na objętość

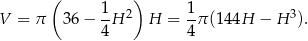
( 1 ) 1 V = π 3 6− -H 2 H = -π (144H − H 3). 4 4

Pozostało wyznaczyć największą wartość funkcji 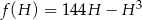3 f (H ) = 144H − H na przedziale 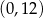(0 ,12) . Liczymy pochodną

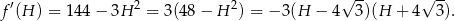
√ -- √ -- f′(H ) = 144 − 3H 2 = 3(48 − H 2) = −3 (H − 4 3)(H + 4 3).

Wykresem tej funkcji jest parabola o ramionach skierowanych w dół, zatem w przedziale 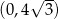√ -- (0 ,4 3) pochodna jest dodatnia, czyli 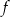f rośnie, a w przedziale 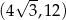√ -- (4 3 ,12) pochodna jest ujemna, czyli funkcja maleje. Największa wartość jest więc przyjmowana dla 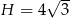√ -- H = 4 3 . Mamy wtedy

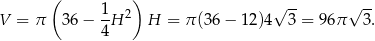
( ) V = π 36 − 1H 2 H = π(36 − 1 2)4√ 3-= 96π √ 3. 4

 
Odpowiedź: 96π √ 3-cm 3

Wersja PDF