Zadanie nr 6052394
Mówimy, że walec jest wpisany w graniastosłup, jeżeli podstawy walca są zawarte w podstawach graniastosłupa, a powierzchnia boczna walca jest styczna do każdej ze ścian bocznych graniastosłupa (zobacz rysunek).
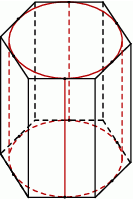
Rozpatrujemy wszystkie graniastosłupy prawidłowe sześciokątne takie, że suma długości promienia i wysokości walca wpisanego w ten graniastosłup jest równa 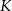 . Oblicz pole powierzchni całkowitej tego z rozważanych graniastosłupów, którego objętość jest największa.
. Oblicz pole powierzchni całkowitej tego z rozważanych graniastosłupów, którego objętość jest największa.
Rozwiązanie
Jeżeli oznaczymy przez  i
i 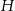 promień i wysokość walca, to wiemy, że
promień i wysokość walca, to wiemy, że
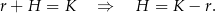
Oznaczmy ponadto przez  długość krawędzi podstawy graniastosłupa.
długość krawędzi podstawy graniastosłupa.
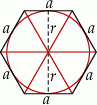
Ponieważ podstawa walca jest kołem wpisanym w sześciokąt foremny w podstawie graniastosłupa, mamy
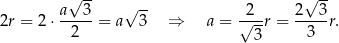
Objętość graniastosłupa jest więc równa
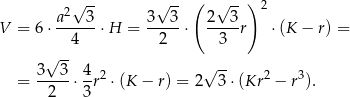
Musimy teraz sprawdzić dla jakiej wartości  funkcja
funkcja
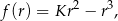
określona dla 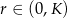 , przyjmuje największą możliwą wartość. Liczymy pochodną
, przyjmuje największą możliwą wartość. Liczymy pochodną
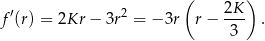
Widać teraz, że pochodna jest dodatnia w przedziale 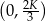 i ujemna w przedziale
i ujemna w przedziale 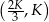 . To oznacza, że funkcja
. To oznacza, że funkcja 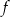 rośnie w przedziale
rośnie w przedziale 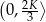 i maleje w przedziale
i maleje w przedziale 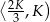 . Największą objętość otrzymamy więc dla
. Największą objętość otrzymamy więc dla 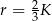 . Wtedy
. Wtedy
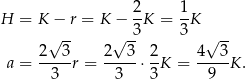
Pole powierzchni całkowitej graniastosłupa jest więc równe
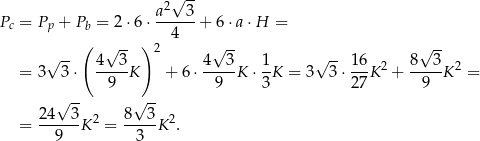
Odpowiedź: