/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema/Największa objętość

Zadanie nr 6439229

Z kartonu w kształcie trójkąta równobocznego o boku długości 120 cm odcięto trzy identyczne czworokąty w narożnikach (zobacz rysunek).

PIC

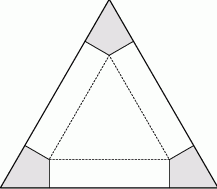
Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób pudełko w kształcie graniastosłupa trójkątnego prostego (bez przykrywki). Oblicz długość krawędzi podstawy tego pudełka, którego objętość jest największa. Oblicz tę objętość.

Wersja PDF

Rozwiązanie

Oznaczmy długość krawędzi podstawy graniastosłupa przez x , a jego wysokość przez h .

PIC

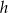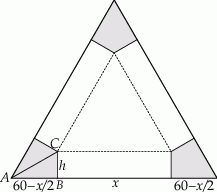
Z trójkąta prostokątnego 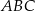ABC mamy

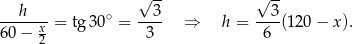
√ -- √ -- --h----= tg 30∘ = --3- ⇒ h = --3(12 0− x). 60− x2 3 6

Objętość pudełka jest więc równa

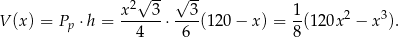
√ -- √ -- x2 3 3 1 2 3 V (x) = Pp ⋅ h =------⋅ ---(120 − x ) = -(12 0x − x ). 4 6 8

Dziedziną tej funkcji jest przedział 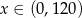x ∈ (0,1 20) . Liczymy pochodną funkcji w nawiasie.

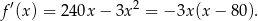
′ 2 f (x) = 240x − 3x = −3x (x − 80).

Wykresem pochodnej jest parabola o ramionach skierowanych w dół, więc pochodna przechodząc przez punkt 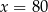x = 80 zmienia znak z dodatniego na ujemny. To oznacza, że funkcja 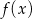f(x) jest rosnąca na lewo od 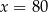x = 80 i malejąca na prawo od tego punktu. W takim razie dla 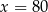x = 80 otrzymamy największą objętość pudełka. Objętość ta jest równa

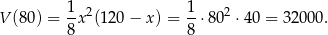
1 2 1 2 V (80) = -x (12 0− x ) = --⋅80 ⋅40 = 3 2000. 8 8

 
Odpowiedź: Długość podstawy: 80 cm, objętość: 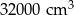3 32000 cm .

Wersja PDF