Zadanie nr 6728102
Suma długości wszystkich krawędzi prostopadłościanu jest równa 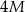 , a jedna z jego ścian na pole powierzchni dwa razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.
, a jedna z jego ścian na pole powierzchni dwa razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.
Rozwiązanie
Szkicujemy prostopadłościan.
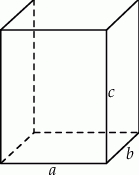
Jeżeli oznaczymy długości krawędzi prostopadłościanu w ten sposób, że ściana o krawędziach 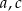 jest dwa razy większa od ściany o krawędziach
jest dwa razy większa od ściany o krawędziach 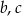 , to mamy
, to mamy
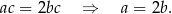
Ponadto z podanej sumy wszystkich krawędzi mamy
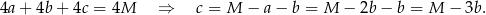
Objętość prostopadłościanu jest więc równa
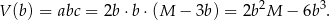
Dziedziną tej funkcji jest przedział 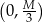 . Liczymy pochodną.
. Liczymy pochodną.
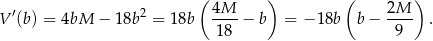
Widać teraz, że pochodna jest dodatnia w przedziale 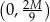 i ujemna w przedziale
i ujemna w przedziale 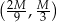 . To oznacza, że funkcja
. To oznacza, że funkcja 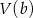 największą wartość przyjmuje dla
największą wartość przyjmuje dla 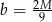 . Mamy wtedy
. Mamy wtedy 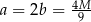 i
i 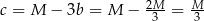 .
.
Pozostało obliczyć pole powierzchni całkowitej
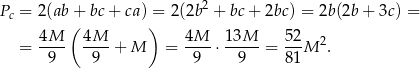
Odpowiedź: