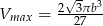Zadanie nr 6798766
Tworząca stożka ma długość 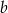 . Wyznacz wysokość tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.
. Wyznacz wysokość tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.
Rozwiązanie
Szkicujemy stożek.
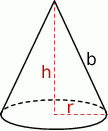
Jeżeli oznaczymy przez  promień podstawy, a przez
promień podstawy, a przez 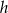 wysokość utworzonego stożka, to mamy
wysokość utworzonego stożka, to mamy
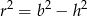
i objętość stożka jest równa
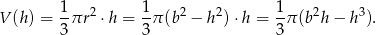
Dziedziną tej funkcji jest przedział 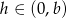 . Liczymy pochodną, aby wyznaczyć jej maksimum.
. Liczymy pochodną, aby wyznaczyć jej maksimum.
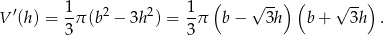
Wykresem 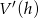 jest parabola o ramionach skierowanych w dół i miejscach zerowych:
jest parabola o ramionach skierowanych w dół i miejscach zerowych: 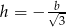 i
i 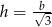 . To oznacza, że pochodna jest dodatnia w przedziale
. To oznacza, że pochodna jest dodatnia w przedziale 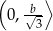 i ujemna w przedziale
i ujemna w przedziale 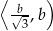 . To z kolei oznacza, że największą objętość stożka otrzymamy dla
. To z kolei oznacza, że największą objętość stożka otrzymamy dla 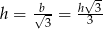 . Objętość ta jest wtedy równa
. Objętość ta jest wtedy równa
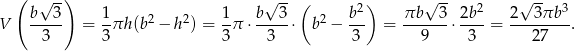
Odpowiedź: 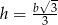 ,
,