Zadanie nr 6816952
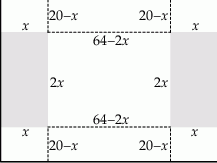
Dany jest prostokątny arkusz kartonu o długości 64 cm i szerokości 40 cm. Po dwóch stronach tego arkusza wycięto prostokąty, w których stosunek boków jest równy 1:2 (zacieniowane prostokąty na rysunku).

Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób prostopadłościenne pudełko (bez przykrywki). Oblicz długości boków wyciętych prostokątów, dla których objętość otrzymanego pudełka jest największa. Oblicz tę objętość.
Rozwiązanie
Jeżeli oznaczymy długość krótszego boku każdego z odciętych prostokątów przez  , to po złożeniu otrzymamy pudełko, które w podstawie ma prostokąt o bokach długości
, to po złożeniu otrzymamy pudełko, które w podstawie ma prostokąt o bokach długości 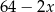 i
i 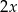 .
.
Wysokość tego pudełka będzie równa 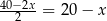 . Musimy zatem znaleźć największą wartość funkcji
. Musimy zatem znaleźć największą wartość funkcji
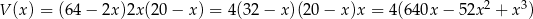
w przedziale 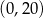 (takie wartości może przyjmować
(takie wartości może przyjmować  ). Liczymy pochodną funkcji w nawiasie.
). Liczymy pochodną funkcji w nawiasie.
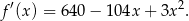
Szukamy teraz miejsc zerowych pochodnej.
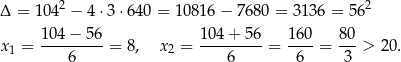
Wykresem pochodnej jest parabola o ramionach skierowanych w górę, więc pochodna przechodząc przez punkt 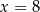 zmienia znak z dodatniego na ujemny. To oznacza, że funkcja
zmienia znak z dodatniego na ujemny. To oznacza, że funkcja 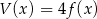 jest rosnąca na lewo od
jest rosnąca na lewo od 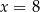 i malejąca na prawo od tego punktu. W takim razie dla
i malejąca na prawo od tego punktu. W takim razie dla 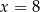 otrzymamy największą objętość pudełka. Objętość ta jest równa
otrzymamy największą objętość pudełka. Objętość ta jest równa
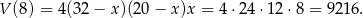
Odpowiedź: Boki prostokąta: 8 cm i 16 cm, objętość: 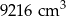 .
.

