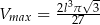Zadanie nr 6994700
Rozpatrujemy wszystkie stożki o tworzącej długości 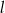 . Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz tę największą objętość.
. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz tę największą objętość.
Rozwiązanie
Szkicujemy stożek.
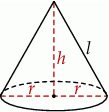
Jeżeli oznaczymy promień podstawy stożka przez  , a jego wysokość przez
, a jego wysokość przez 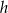 , to mamy
, to mamy
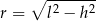
i objętość bryły jest równa
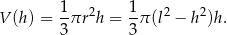
Wyznaczenie bryły o największej objętości sprowadza się więc do wyznaczenia największej wartości funkcji
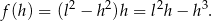
Liczymy pochodną tej funkcji
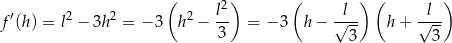
Dziedziną funkcji 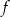 jest przedział
jest przedział 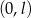 i w tym przedziale pochodna ma jedno miejsce zerowe
i w tym przedziale pochodna ma jedno miejsce zerowe 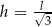 . Ponadto na lewo od tego miejsca zerowego pochodna jest dodatnia, a na prawo jest ujemna. To oznacza, że funkcja
. Ponadto na lewo od tego miejsca zerowego pochodna jest dodatnia, a na prawo jest ujemna. To oznacza, że funkcja 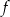 rośnie w przedziale
rośnie w przedziale 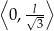 i maleje w przedziale
i maleje w przedziale 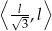 . W takim razie największą objętość stożka otrzymamy dla
. W takim razie największą objętość stożka otrzymamy dla 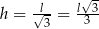 . Wtedy
. Wtedy
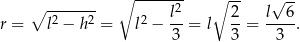
Objętość jest wtedy równa
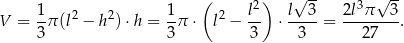
Odpowiedź: 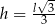 ,
, 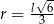 ,
,