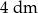Zadanie nr 7463453
W stożek, którego wysokość ma długość 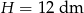 , a promień jego podstawy ma długość
, a promień jego podstawy ma długość 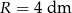 wpisano walec, o podstawach równoległych do podstawy stożka. Jakie powinny być wymiary walca, aby jego objętość była największa?
wpisano walec, o podstawach równoległych do podstawy stożka. Jakie powinny być wymiary walca, aby jego objętość była największa?
Rozwiązanie
Naszkicujmy sobie przekrój osiowy opisanej sytuacji
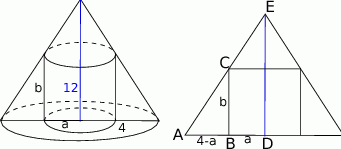
Z podobieństwa trójkątów 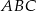 i
i 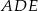 mamy
mamy
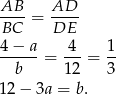
Objętość walca wynosi więc
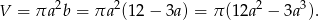
Pozostało wyznaczyć dla jakiego  w przedziale
w przedziale 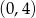 wartość funkcji
wartość funkcji 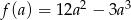 jest największa. Liczymy pochodną
jest największa. Liczymy pochodną
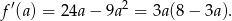
Widać stąd, że na przedziale 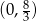 funkcja jest rosnąca (pochodna jest dodatnia), a na przedziale
funkcja jest rosnąca (pochodna jest dodatnia), a na przedziale 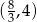 malejąca (pochodna jest ujemna). Zatem największą objętość otrzymamy dla
malejąca (pochodna jest ujemna). Zatem największą objętość otrzymamy dla 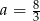 . Wtedy
. Wtedy 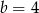 .
.
Odpowiedź: promień podstawy: 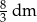 , wysokość:
, wysokość: