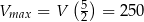Zadanie nr 8583723

Rozpatrujemy wszystkie możliwe drewniane szkielety o kształcie przedstawionym na rysunku, wykonane z listewek. Każda z tych listewek ma kształt prostopadłościanu o podstawie kwadratu o boku długości . Wymiary szkieletu zaznaczono na rysunku.

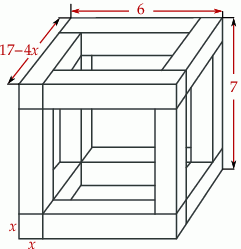
Wyznacz objętość 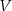drewna potrzebnego do budowy szkieletu jako funkcję zmiennej .
Wyznacz dziedzinę funkcji .
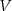Oblicz tę wartość , dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja 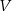osiąga wartość największą. Oblicz tę największą objętość.

Rozwiązanie

Wszystkie listewki mają ten sam przekrój o polu 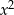, więc wystarczy ustalić jaka jest ich łączna długość. Są 4 pionowe listewki długości 7, cztery długości 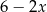(poziome na rysunku) i 4 długości 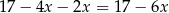(skośne na rysunku). Ich łączna długość jest równa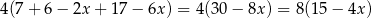
$4(7 + 6 − 2x + 17 − 6x ) = 4(30 − 8x) = 8(15− 4x)$

i objętość całego szkieletu jest równa

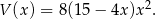
$V (x) = 8(15 − 4x )x2.$

Odpowiedź: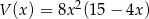
Wymiary szkieletu przedstawionego na rysunku muszą spełniać nierówności
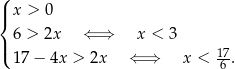
$( | x > 0 { | 6 > 2x ⇐ ⇒ x < 3 ( 17 − 4x > 2x ⇐ ⇒ x < 17. 6$

Dziedziną funkcji 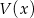jest więc przedział .
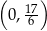Odpowiedź: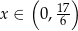
Liczymy pochodną funkcji
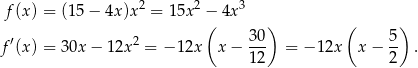
$2 2 3 f (x) = (15 − 4x )x = 15x −( 4x ) ( ) ′ 2 30 5 f (x) = 30x − 1 2x = − 12x x− --- = − 12x x − -- . 12 2$

Widzimy teraz, że pochodna jest dodatnia w przedziale 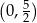i ujemna w przedziale 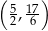. To oznacza, że funkcja 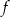(a więc też funkcja 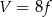) rośnie w przedziale 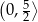i maleje w przedziale 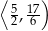. W takim razie największą objętość szkieletu otrzymamy dla 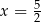i jest ona równa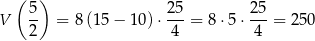

$( ) V 5- = 8 (15− 10)⋅ 25-= 8⋅5 ⋅ 25-= 250 2 4 4$

Odpowiedź: