/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema/Największa objętość

Zadanie nr 8971705

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa jest trójkąt prostokątny, w którym tangens jednego z kątów ostrych jest równy 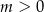m > 0 . Wszystkie krawędzie boczne ostrosłupa mają długość 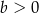b > 0 . Jakie powinno być pole podstawy ostrosłupa, aby jego objętość była największa? Oblicz tę największą objętość.

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.