Zadanie nr 9031363
Rozpatrujemy wszystkie stożki, których pole powierzchni całkowitej jest równe 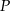 . Oblicz wysokość i promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.
. Oblicz wysokość i promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.
Rozwiązanie
Niech 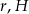 i
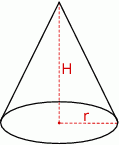
i 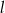 oznaczają odpowiednio promień podstawy, wysokość i długość tworzącej stożka.
oznaczają odpowiednio promień podstawy, wysokość i długość tworzącej stożka.
Z podanego pola powierzchni całkowitej mamy
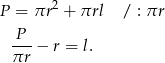
Z drugiej strony 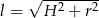 , więc
, więc
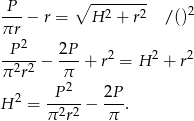
Nas interesuje objętość stożka 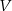 . Ponieważ
. Ponieważ 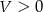 , wystarczy ustalić kiedy
, wystarczy ustalić kiedy 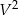 przyjmuje wartość największą.
przyjmuje wartość największą.
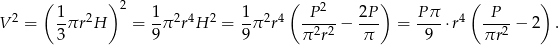
Wystarczy teraz ustalić jaka jest największa możliwa wartość funkcji
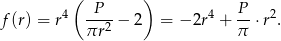
Liczymy pochodną
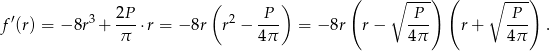
Dziedziną tej funkcji jest przedział 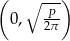 (bo musi być
(bo musi być 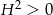 ). Widać z powyższego wzoru, że pochodna jest dodatnia w przedziale
). Widać z powyższego wzoru, że pochodna jest dodatnia w przedziale 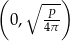 i ujemna w przedziale
i ujemna w przedziale 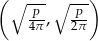 . To oznacza, że funkcja
. To oznacza, że funkcja 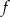 jest rosnąca na przedziale
jest rosnąca na przedziale 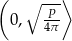 i malejąca na przedziale
i malejąca na przedziale 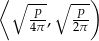 . W takim razie największą objętość stożka otrzymamy dla
. W takim razie największą objętość stożka otrzymamy dla 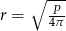 . Mamy wtedy
. Mamy wtedy
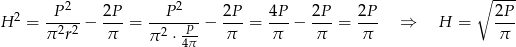
i objętość jest równa
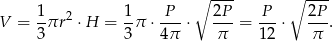
Odpowiedź: 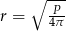 ,
, 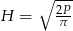 ,
,