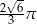Zadanie nr 9226229
Z papierowego koła o promieniu 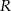 wycięto wycinek kołowy, który jest powierzchnią boczną stożka o maksymalnej objętości. Jaka była miara kąta środkowego
wycięto wycinek kołowy, który jest powierzchnią boczną stożka o maksymalnej objętości. Jaka była miara kąta środkowego  wyciętego wycinka? Wynik podaj w radianach.
wyciętego wycinka? Wynik podaj w radianach.
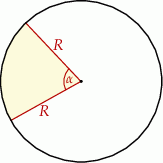
Rozwiązanie
Szkicujemy stożek.
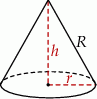
Jeżeli oznaczymy przez  promień podstawy, a przez
promień podstawy, a przez 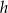 wysokość utworzonego stożka, to mamy
wysokość utworzonego stożka, to mamy
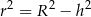
i objętość stożka jest równa
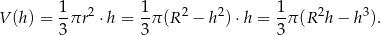
Dziedziną tej funkcji jest przedział 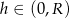 . Liczymy pochodną, aby wyznaczyć jej maksimum.
. Liczymy pochodną, aby wyznaczyć jej maksimum.
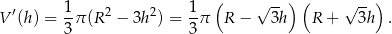
Wykresem 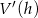 jest parabola o ramionach skierowanych w dół i miejscach zerowych:
jest parabola o ramionach skierowanych w dół i miejscach zerowych: 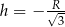 i
i 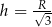 . To oznacza, że pochodna jest dodatnia w przedziale
. To oznacza, że pochodna jest dodatnia w przedziale 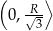 i ujemna w przedziale
i ujemna w przedziale 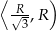 . To z kolei oznacza, że największą objętość stożka otrzymamy dla
. To z kolei oznacza, że największą objętość stożka otrzymamy dla 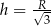 . Długość okręgu w podstawie stożka jest wtedy równa
. Długość okręgu w podstawie stożka jest wtedy równa
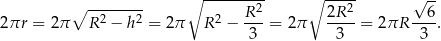
Interesujący nas kąt  spełnia więc proporcję
spełnia więc proporcję
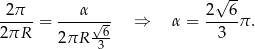
Odpowiedź: