Zadanie nr 9389470
Suma długości wszystkich krawędzi graniastosłupa prawidłowego sześciokątnego jest równa 36. Jakie są wymiary graniastosłupa o największej objętości?
Rozwiązanie
Zaczynamy oczywiście od schematycznego rysunku.
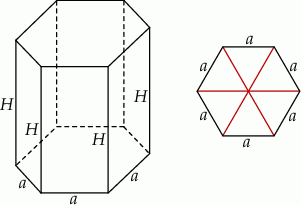
Jeżeli oznaczmy krawędź podstawy graniastosłupa przez  , a wysokość przez
, a wysokość przez 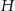 , to mamy
, to mamy
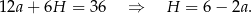
Sześciokąt foremny w podstawie graniastosłupa składa się z 6 trójkątów równobocznych o boku  , więc objętość graniastosłupa wyraża się wzorem
, więc objętość graniastosłupa wyraża się wzorem
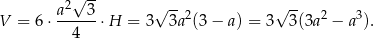
Pozostało sprawdzić, dla jakiego 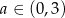 (bo
(bo 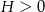 ) funkcja
) funkcja 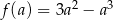 przyjmuje wartość największą. Liczymy pochodną
przyjmuje wartość największą. Liczymy pochodną
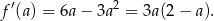
Ponieważ pochodna jest parabolą o ramionach skierowanych w dół, więc funkcja 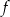 jest rosnąca na przedziale
jest rosnąca na przedziale 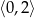 (bo pochodna jest dodatnia) i malejąca na przedziale
(bo pochodna jest dodatnia) i malejąca na przedziale 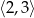 (pochodna jest ujemna). Zatem największą wartość
(pochodna jest ujemna). Zatem największą wartość 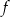 przyjmuje w punkcie
przyjmuje w punkcie 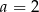 . Wysokość graniastosłupa jest wtedy równa
. Wysokość graniastosłupa jest wtedy równa
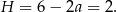
Odpowiedź: Krawędź podstawy: 2, wysokość: 2.

