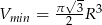Zadanie nr 7657041
Na półkuli o promieniu 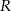 opisano stożek w ten sposób, że środek podstawy stożka pokrywa się ze środkiem kuli. Jaka jest najmniejsza możliwa objętość tego stożka?
opisano stożek w ten sposób, że środek podstawy stożka pokrywa się ze środkiem kuli. Jaka jest najmniejsza możliwa objętość tego stożka?
Rozwiązanie
Szkicujemy opisaną sytuację.
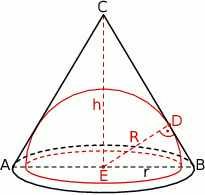
Spróbujemy obliczyć objętość stożka w zależności od jego wysokości 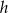 .
.
Zauważmy, że promień 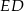 jest wysokością w trójkącie prostokątnym
jest wysokością w trójkącie prostokątnym 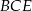 . Porównując dwa wzory na pole tego trójkąta mamy więc
. Porównując dwa wzory na pole tego trójkąta mamy więc
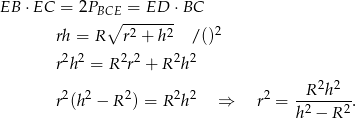
Objętość stożka jest więc równa
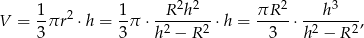
gdzie 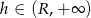 . Aby wyznaczyć stożek o najmniejszej możliwej objętości wystarczy więc wyznaczyć najmniejszą wartość funkcji
. Aby wyznaczyć stożek o najmniejszej możliwej objętości wystarczy więc wyznaczyć najmniejszą wartość funkcji
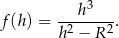
Liczymy pochodną
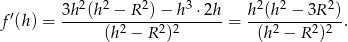
Widać teraz, że pochodna jest ujemna w przedziale 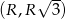 i dodatnia w przedziale
i dodatnia w przedziale 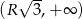 . To oznacza, że funkcja
. To oznacza, że funkcja 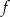 jest malejąca w przedziale
jest malejąca w przedziale 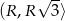 i rosnąca w przedziale
i rosnąca w przedziale 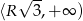 . Najmniejszą objętość otrzymamy więc dla
. Najmniejszą objętość otrzymamy więc dla 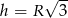 . Objętość stożka jest wtedy równa
. Objętość stożka jest wtedy równa
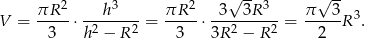
Odpowiedź: