/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema

Zadanie nr 2546576

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma długości dwóch boków trójkąta jest równa 4, a kąt zawarty między nimi ma miarę 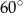6 0∘ . Oblicz najmniejszą możliwą wartość obwodu trójkąta.

Rozwiązanie

Szkicujemy trójkąt.

PIC

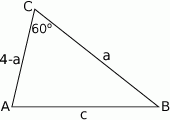
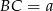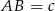Jeżeli oznaczmy BC = a i AB = c to z założenia 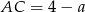AC = 4 − a . Długość boku 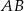AB możemy obliczyć z twierdzenia cosinusów.

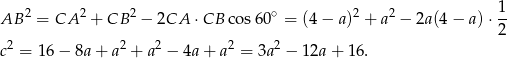
AB 2 = CA 2 + CB 2 − 2CA ⋅CB co s60∘ = (4− a )2 + a2 − 2a(4 − a) ⋅ 1 2 c2 = 1 6− 8a+ a2 + a 2 − 4a + a2 = 3a2 − 12a+ 16.

Obwód trójkąta jest więc równy

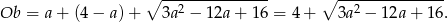
∘ --------------- ∘ --------------- Ob = a + (4 − a) + 3a2 − 12a+ 16 = 4 + 3a 2 − 1 2a+ 16.

Wyrażenie to będzie miało najmniejszą możliwą wartość, gdy najmniejszą wartość będzie miał trójmian pod pierwiastkiem

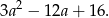
2 3a − 1 2a+ 16.

Wykresem tego trójmianu jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość otrzymamy w wierzchołku, czyli dla

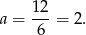
a = 12-= 2. 6

Obwód jest wtedy równy

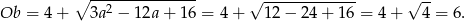
--------------- ∘ 2 √ ------------- √ -- Ob = 4 + 3a − 12a+ 16 = 4 + 12 − 24 + 16 = 4+ 4 = 6.

 
Odpowiedź: 6

Wersja PDF