Zadanie nr 2640342
Dany jest okrąg o środku 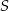 i promieniu 12. Rozpatrujemy pary okręgów: jeden o środku
i promieniu 12. Rozpatrujemy pary okręgów: jeden o środku 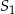 i promieniu
i promieniu  oraz drugi o środku
oraz drugi o środku 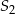 i promieniu
i promieniu 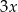 , o których wiadomo, że spełniają jednocześnie następujące warunki:
, o których wiadomo, że spełniają jednocześnie następujące warunki:
– rozważane dwa okręgi są styczne zewnętrznie;
– obydwa rozważane okręgi są styczne wewnętrznie do okręgu o środku 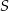 i promieniu 12;
i promieniu 12;
– punkty: 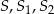 nie leżą na jednej prostej.
nie leżą na jednej prostej.
Zapisz pole trójkąta 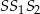 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.
. Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.
Rozwiązanie
Szkicujemy opisaną sytuację.
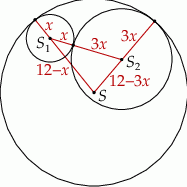
Z rysunku powinno być jasne, że 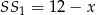 ,
, 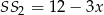 i
i 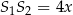 .
.
Pole trójkąta o bokach 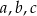 można obliczyć ze wzoru Herona
można obliczyć ze wzoru Herona
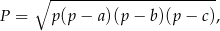
gdzie 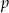 – jest połową obwodu trójkąta.
– jest połową obwodu trójkąta.
W naszej sytuacji mamy
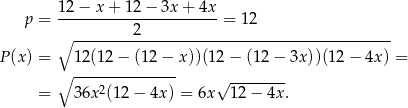
Dziedziną tej funkcji jest przedział 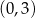 (łatwo sprawdzić, że dla
(łatwo sprawdzić, że dla 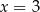 punkty
punkty 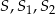 leżą na jednej prostej).
leżą na jednej prostej).
Liczymy teraz pochodną funkcji
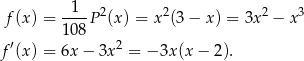
Widać teraz, że pochodna jest dodatnia na przedziale 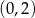 i ujemna na przedziale
i ujemna na przedziale 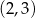 . To oznacza, że funkcja
. To oznacza, że funkcja 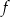 (a więc też funkcja
(a więc też funkcja 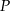 ) rośnie na przedziale
) rośnie na przedziale 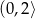 i maleje
i maleje 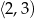 . W takim razie największe pole otrzymamy dla
. W takim razie największe pole otrzymamy dla 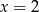 . Jest ono wtedy równe
. Jest ono wtedy równe
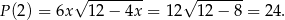
Boki trójkąta mają wtedy długości 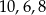 (jest to więc trójkąt prostokątny).
(jest to więc trójkąt prostokątny).
Odpowiedź: 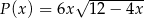 dla
dla 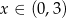 ,
, 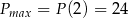 , boki: 6, 8, 10.
, boki: 6, 8, 10.

