Zadanie nr 3020043
- Wykaż, że dla dowolnych liczb nieujemnych
 i
i 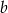 spełniona jest nierówność
spełniona jest nierówność 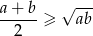
- W zbiorze prostokątów wpisanych w okrąg o promieniu
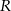 znajdź prostokąt o największym polu.
znajdź prostokąt o największym polu.
Rozwiązanie
- Przekształcamy równoważnie daną nierówność
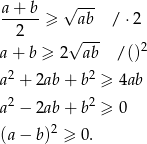
Otrzymana nierówność jest oczywiście spełniona, a przekształcaliśmy przy pomocy równoważności, więc dana nierówność też musi być prawdziwa. Zauważmy jeszcze, że nierówność staje się równością tylko w jednej sytuacji: gdy
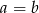 .
. - Oznaczmy przez
 i
i 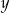 długości boków prostokąta wpisanego w okrąg o promieniu
długości boków prostokąta wpisanego w okrąg o promieniu 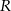 .
. 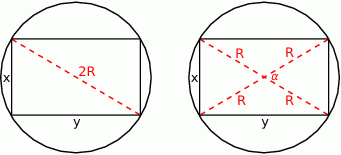
Zatem na mocy twierdzenia Pitagorasa
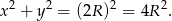
Dalszą część rozwiązania przeprowadzimy na kilka sposobów..
Sposób I
Jeżeli podstawimy w nierówności z podpunktu a) liczby
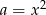 i
i 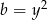 mamy
mamy 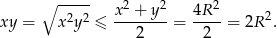
Zatem pole prostokąta nie może być większe niż
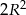 i wiemy, że równość może zachodzić tylko w jednym przypadku, gdy
i wiemy, że równość może zachodzić tylko w jednym przypadku, gdy 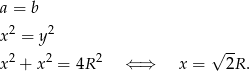
Sposób II
Analogicznie jak w poprzednim podpunkcie, można uzasadnić nierówność
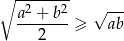
(nierówność między średnimi: kwadratową i geometryczną) i podobnie jak w przypadku nierówności z podpunktu a) równość zachodzi dokładnie wtedy, gdy
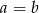 . Na mocy tej nierówności mamy
. Na mocy tej nierówności mamy 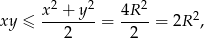
przy czym równość zachodzi wtedy i tylko wtedy, gdy
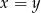 .
. Sposób III
Wiemy, że
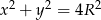 , a chcemy znaleźć maksimum funkcji
, a chcemy znaleźć maksimum funkcji 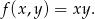
Ponieważ funkcja
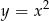 jest rosnąca dla
jest rosnąca dla 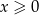 , więc zamiast szukać maksimum funkcji
, więc zamiast szukać maksimum funkcji 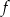 , możemy szukać maksimum funkcji
, możemy szukać maksimum funkcji ![2 2 2 2 2 2 g(x ,y ) = [f(x,y)] = x y = x (4R − x ).](https://img.zadania.info/zad/3020043/HzadR21x.gif)
Jeżeli myślimy o tym wyrażeniu jak o funkcji zmiennej
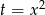 to wykresem tej funkcji jest parabola o ramionach skierowanych w dół. Zatem największą wartość przyjmuje ona w wierzchołku, czyli dokładnie w środku między pierwiastkami
to wykresem tej funkcji jest parabola o ramionach skierowanych w dół. Zatem największą wartość przyjmuje ona w wierzchołku, czyli dokładnie w środku między pierwiastkami 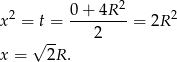
Sposób IV
Oznaczmy miarę kąta między przekątnymi prostokąta przez
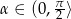 . Ze wzoru na pole równoległoboku z przekątnymi mamy
. Ze wzoru na pole równoległoboku z przekątnymi mamy 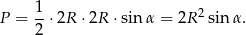
Ponieważ funkcja
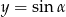 jest rosnąca w pierwszej ćwiartce, największą wartość pola otrzymamy gdy,
jest rosnąca w pierwszej ćwiartce, największą wartość pola otrzymamy gdy, 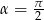 . Wtedy czworokąt jest rombem wpisanym w okrąg, czyli musi to być kwadrat.
. Wtedy czworokąt jest rombem wpisanym w okrąg, czyli musi to być kwadrat.
Odpowiedź: Kwadrat o boku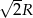 .
.

