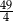/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema

Zadanie nr 4244758

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma długości dwóch sąsiednich boków w pewnym trójkącie jest równa 14, a kąt między tymi bokami ma miarę 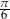π6- . Wyznacz długości boków trójkąta tak, aby jego pole było największe. Oblicz pole tego trójkąta.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

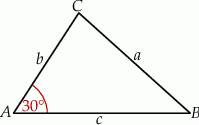
Pole trójkąta jest równe (korzystamy ze wzoru na pole z sinusem)

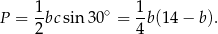
P = 1bc sin 30∘ = 1b(14 − b). 2 4

Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w dół, więc największą wartość pola otrzymamy w wierzchołku paraboli, czyli dla 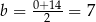b = 0+214-= 7 (w środku między pierwiastkami). Wtedy 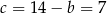c = 14 − b = 7 i pole jest równe

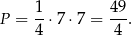
1- 49- P = 4 ⋅7⋅7 = 4 .

Obliczmy jeszcze długość trzeciego boku trójkąta – korzystamy z twierdzenia cosinusów.

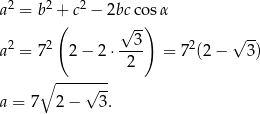
a2 = b2 + c2 − 2bcco sα ( √ --) 2 2 --3- 2 √ -- a = 7 2 − 2 ⋅ 2 = 7 (2 − 3) ∘ -------- √ -- a = 7 2− 3.

 
Odpowiedź: Boki: 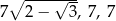∘ ----√--- 7 2 − 3, 7, 7 . Pole: 449

Wersja PDF