Zadanie nr 4801096
Wewnątrz prostokąta 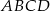 o wymiarach
o wymiarach 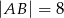 i
i 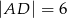 wybrano dwa punkty
wybrano dwa punkty 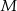 i
i 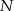 takie, że
takie, że 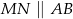 oraz
oraz 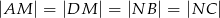 . Przy jakiej odległości punktów
. Przy jakiej odległości punktów 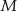 i
i 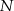 suma kwadratów długości odcinków
suma kwadratów długości odcinków 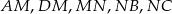 jest najmniejsza?
jest najmniejsza?
Rozwiązanie
Rozpoczynamy od rysunku.
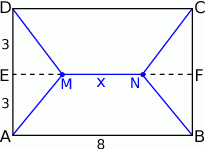
Jeżeli oznaczymy 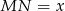 to ponieważ trójkąty
to ponieważ trójkąty 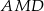 i
i 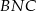 są przystające, mamy
są przystające, mamy
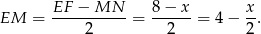
Możemy teraz wyliczyć interesującą nas sumę kwadratów
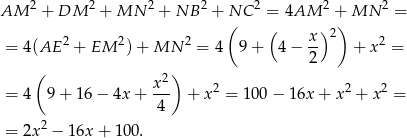
Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych do góry, więc najmniejszą wartość otrzymamy w wierzchołku, czyli dla 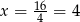 .
.
Odpowiedź: