Zadanie nr 4948674
W trójkącie o obwodzie 14 jeden z boków jest dwa razy dłuższy od drugiego boku. Oblicz cosinus najmniejszego kąta, tego spośród trójkątów spełniających podany warunek, w którym suma kwadratów długości boków jest najmniejsza.
Rozwiązanie
Oznaczmy długości boków szukanego trójkąta przez 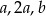 . W takim razie
. W takim razie
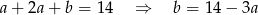
i suma kwadratów długości boków jest równa
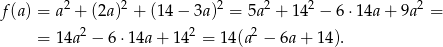
Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość przyjmuje w wierzchołku, czyli dla 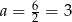 . Wtedy pozostałe boki mają długości
. Wtedy pozostałe boki mają długości 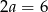 oraz
oraz 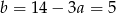 .
.
Zwróćmy uwagę na to, że nie przejmowaliśmy się dziedziną funkcji 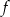 – nie musimy tego robić, bo widać, że otrzymane 3 liczby są rzeczywiście długościami boków trójkąta spełniającego warunki zadania, więc otrzymane
– nie musimy tego robić, bo widać, że otrzymane 3 liczby są rzeczywiście długościami boków trójkąta spełniającego warunki zadania, więc otrzymane  na pewno należy do dziedziny.
na pewno należy do dziedziny.
W trójkącie najmniejszy kąt leży naprzeciwko najkrótszego boku, więc musimy wyliczyć cosinus kąta leżącego naprzeciwko boku długości 3.
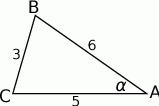
Stosujemy twierdzenie cosinusów.
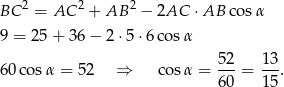
Odpowiedź: