Zadanie nr 5577813
Dany jest trójkąt równoboczny 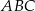 o boku długości
o boku długości  . Punkty
. Punkty 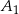 ,
, 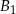 i
i 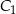 należą do boków
należą do boków 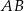 ,
, 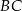 i
i 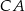 , przy czym
, przy czym 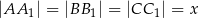 .
.
- Wyraź pole trójkąta
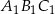 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji.
. Wyznacz dziedzinę tej funkcji. - Wyznacz wartość
 , dla której pole trójkąta
, dla której pole trójkąta 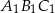 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole.
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

