Zadanie nr 6118858
Spośród wszystkich trapezów, w których iloczyn długości podstaw jest równy 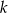 , a pole jest równe
, a pole jest równe 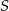 wybrano ten, który ma najdłuższą wysokość. Wykaż, że przekątne wybranego trapezu dzielą się na połowy.
wybrano ten, który ma najdłuższą wysokość. Wykaż, że przekątne wybranego trapezu dzielą się na połowy.
Rozwiązanie
Oznaczmy przez  i
i 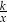 długości podstaw trapezu, a przez
długości podstaw trapezu, a przez 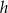 jego wysokość.
jego wysokość.
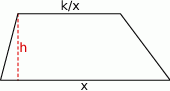
Pole trapezu jest równe
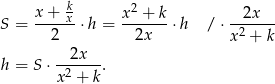
Musimy teraz wyznaczyć największą możliwą wartość funkcji
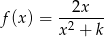
w przedziale 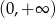 . Liczymy pochodną
. Liczymy pochodną
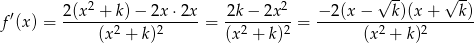
Widać teraz, że pochodna jest dodatnia dla 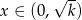 i ujemna dla
i ujemna dla 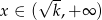 . To oznacza, że funkcja
. To oznacza, że funkcja 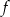 jest rosnąca w przedziale
jest rosnąca w przedziale 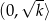 i malejąca w przedziale
i malejąca w przedziale 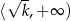 . Najdłuższą wysokość otrzymamy więc dla
. Najdłuższą wysokość otrzymamy więc dla 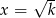 .
.
Zauważmy teraz, że jeżeli 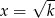 , to druga podstawa trapezu ma długość
, to druga podstawa trapezu ma długość
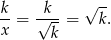
To z kolei oznacza, że trapez ten jest równoległobokiem, co w szczególności oznacza, że jego przekątne dzielą się na połowy.

