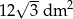Zadanie nr 6899596
Okno na poddaszu ma mieć kształt trapezu równoramiennego, którego krótsza podstawa i ramiona mają długość po 4 dm. Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby do pomieszczenia wpadało przez to okno jak najwięcej światła, czyli aby pole powierzchni okna było największe. Oblicz to pole.
Rozwiązanie
Szkicujemy trapez równoramienny.
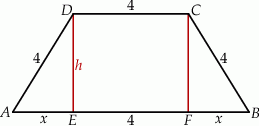
Sposób I
Oznaczmy 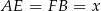 . Wtedy wysokość trapezu jest równa
. Wtedy wysokość trapezu jest równa
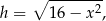
a jego pole
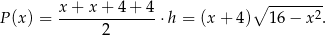
Pozostało więc wyznaczyć największą możliwą wartość funkcji 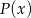 dla
dla 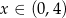 (prawy koniec przedziału jest konsekwencją nierówności
(prawy koniec przedziału jest konsekwencją nierówności 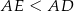 ). Liczymy pochodną (ze wzoru na pochodną iloczynu)
). Liczymy pochodną (ze wzoru na pochodną iloczynu)
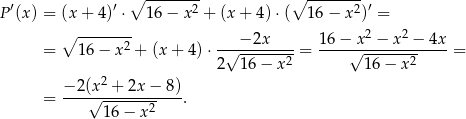
Rozkładamy teraz trójmian w liczniku.
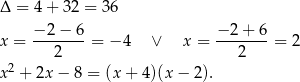
Mamy zatem
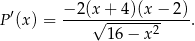
Widać teraz, że pochodna jest dodatnia dla 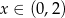 i ujemna dla
i ujemna dla 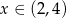 . W takim razie funkcja
. W takim razie funkcja 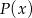 rośnie w przedziale
rośnie w przedziale 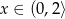 i maleje w przedziale
i maleje w przedziale 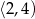 . Największą wartość tej funkcji otrzymamy więc dla
. Największą wartość tej funkcji otrzymamy więc dla 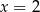 . Pole trapezu jest wtedy równe
. Pole trapezu jest wtedy równe

Sposób II
Tak jak w poprzednim sposobie dochodzimy do zależności
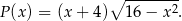
Ponieważ 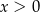 możemy ten wzór zapisać w postaci
możemy ten wzór zapisać w postaci
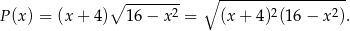
Funkcja 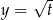 jest rosnąca, więc wystarczy ustalić dla jakiej wartości
jest rosnąca, więc wystarczy ustalić dla jakiej wartości 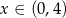 największą wartość przyjmuje funkcja
największą wartość przyjmuje funkcja
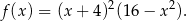
Liczymy pochodną
+ (x + 4 )(1 6− x ) = = 2(x + 4)(1 6− x 2)+ (x + 4 )2 ⋅(− 2x) = 2 2 = 2(x + 4)(1 6− x − x (x+ 4)) = − 4(x + 4)(x + 2x − 8 ).](https://img.zadania.info/zad/6899596/HzadR23x.gif)
Rozkładamy teraz trójmian w ostatnim nawiasie.
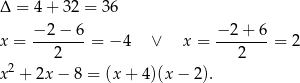
Mamy zatem
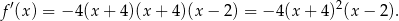
Widać teraz, że pochodna jest dodatnia dla 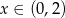 i ujemna dla
i ujemna dla 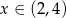 . W takim razie funkcja
. W takim razie funkcja 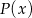 rośnie w przedziale
rośnie w przedziale 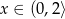 i maleje w przedziale
i maleje w przedziale 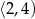 . Największą wartość tej funkcji otrzymamy więc dla
. Największą wartość tej funkcji otrzymamy więc dla 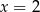 . Pole trapezu jest wtedy równe
. Pole trapezu jest wtedy równe

Sposób III
Tak jak w poprzednim sposobie sprowadzamy rozwiązanie zadania do wyznaczenia największej wartości funkcji
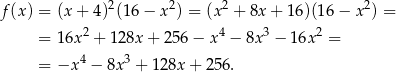
w przedziale 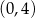 . Tym razem pochodną obliczymy jednak nie korzystając ze wzoru na pochodną złożenia.
. Tym razem pochodną obliczymy jednak nie korzystając ze wzoru na pochodną złożenia.
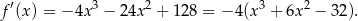
Aby rozłożyć otrzymany wielomian szukamy jego pierwiastków wymiernych. Sprawdzając dzielniki wyrazu wolnego, łatwo znaleźć pierwiastek 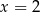 . Dzielimy więc ten wielomian przez
. Dzielimy więc ten wielomian przez 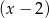 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
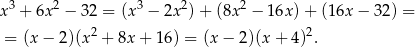
Mamy zatem
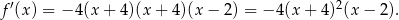
Dalszą część rozwiązania prowadzimy tak jak w poprzednim sposobie.
Sposób IV
Rozwiązanie zadania znacznie się uprości jeżeli oznaczymy 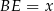 .
.
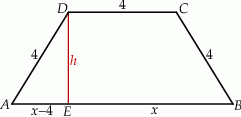
Mamy wtedy
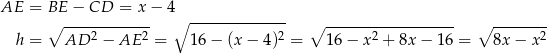
i pole trapezu jest równe
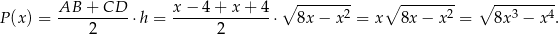
Badamy teraz funkcję
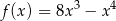
określoną dla 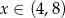 (bo
(bo 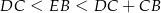 ). Liczymy pochodną
). Liczymy pochodną
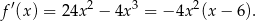
Widać teraz, że pochodna jest dodatnia w przedziale 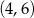 i ujemna w przedziale
i ujemna w przedziale 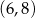 . To oznacza, że funkcja
. To oznacza, że funkcja 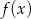 rośnie w przedziale
rośnie w przedziale 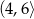 i maleje w przedziale
i maleje w przedziale 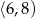 . W takim razie największą wartość pola otrzymamy dla
. W takim razie największą wartość pola otrzymamy dla 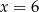 . Pole jest wtedy równe
. Pole jest wtedy równe
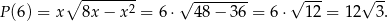
Odpowiedź: Podstawa: 8 dm, pole: