/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema

Zadanie nr 8219797

Dodaj do ulubionych
Dodaj do rozwiązanych

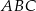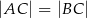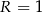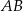Rozpatrujemy wszystkie trójkąty równoramienne ostrokątne ABC (|AC | = |BC | ), na których opisano okrąg o promieniu R = 1 . Niech x oznacza odległość środka okręgu od podstawy AB trójkąta.

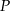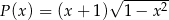  • Wykaż, że pole P każdego z tych trójkątów, jako funkcja długości x , wyraża się wzorem √ -----2- P(x) = (x+ 1) 1− x .
  • Wyznacz dziedzinę funkcji P .
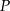  • Oblicz długość odcinka x tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.