/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema

Zadanie nr 9141189

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest trójkąt, w którym suma długości boku i wysokości opuszczonej na ten bok jest równa 8. Funkcja 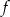f przyporządkowuje długości tego boku – pole trójkąta. Wyznacz wzór tej funkcji, jej dziedzinę, największą wartość, oraz zbiór wartości funkcji.

Rozwiązanie

Oznaczmy przez a długość boku trójkąta.

PIC

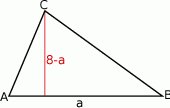
Wtedy wysokość opuszczona na ten bok ma długość 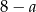8 − a i pole trójkąta jest równe

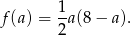
f(a) = 1a(8 − a). 2

Dziedziną tej funkcji jest przedział 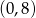(0,8 ) . Jej wykresem jest parabola o ramionach skierowanych w dół, więc największą wartość otrzymamy w wierzchołku, czyli dla 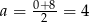a = 0+-8-= 4 2 (w środku między pierwiastkami). Pole jest wtedy równe

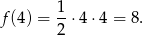
1 f(4 ) = --⋅4 ⋅4 = 8. 2

Ponieważ

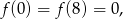
f(0) = f(8 ) = 0,

zbiorem wartości funkcji jest przedział 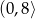(0,8⟩ .  
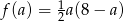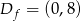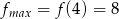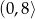Odpowiedź: 1 f(a) = 2a(8 − a) , Df = (0 ,8) , fmax = f(4) = 8 , zbiór wartości: (0 ,8 ⟩ .

Wersja PDF