/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema

Zadanie nr 9382356

Dodaj do ulubionych
Dodaj do rozwiązanych

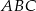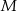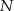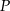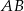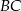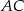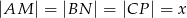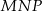Obwód trójkąta równobocznego ABC jest równy 12 cm. Punkty M , N i P należą odpowiednio do boków AB , BC , AC tego trójkąta przy czym |AM | = |BN | = |CP | = x . Zbadaj dla jakiej wartości x , pole trójkąta MNP będzie najmniejsze. Znajdź wartość tego pola.

Rozwiązanie

Naszkicujmy opisaną sytuację.

PIC

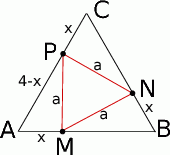
Otrzymany trójkąt 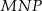MNP jest trójkątem równobocznym, jego bok możemy wyliczyć z twierdzenia cosinusów

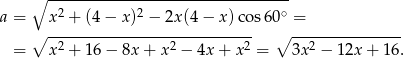
∘ --------------------------------- a = x2 + (4 − x)2 − 2x(4 − x) cos6 0∘ = ∘ ---------------------------- ∘ --------------- = x2 + 16 − 8x + x 2 − 4x + x 2 = 3x 2 − 1 2x+ 16.

Pole trójkąta 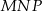MNP wynosi

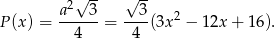
√ -- √ -- a2 3 3 P (x) = ------= ----(3x 2 − 12x + 16). 4 4

Pozostało wyznaczyć wartość 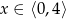x ∈ ⟨0,4⟩ , dla której funkcja 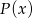P(x) przyjmuje najmniejszą wartość. Ponieważ wykresem tej funkcji jest parabola o ramionach skierowanych w górę, więc przyjmuje ona wartość najmniejszą w wierzchołku, czyli dla 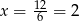x = 12 = 2 6 . Pole wynosi wtedy

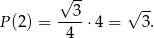
√ -- --3- √ -- P (2) = 4 ⋅4 = 3.

 
Odpowiedź: 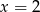x = 2 , pole: √ 3-

Wersja PDF