Zadanie nr 9733258
Suma długości dwóch boków trójkąta wynosi 6 cm, a miara kąta pomiędzy tymi bokami wynosi 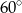 . Jaką najmniejszą wartość ma obwód tego trójkąta.
. Jaką najmniejszą wartość ma obwód tego trójkąta.
Rozwiązanie
Przy oznaczeniach z rysunku, na mocy twierdzenia cosinusów mamy
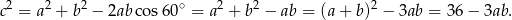
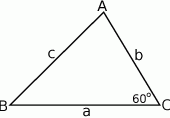
Pytanie jest zatem następujące: wiemy, że 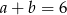 , jaka jest najmniejsza wartość wyrażenia
, jaka jest najmniejsza wartość wyrażenia 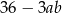 ? Liczymy
? Liczymy
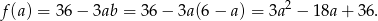
Dziedziną tej funkcji jest przedział 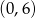 . Wykresem tej funkcji jest parabola o ramionach skierowanych do góry i wierzchołku w punkcie
. Wykresem tej funkcji jest parabola o ramionach skierowanych do góry i wierzchołku w punkcie
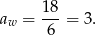
Zatem minimalny obwód otrzymamy dla trójkąta równobocznego o boku 3 cm.
Odpowiedź: 9 cm

