Zadanie nr 3884641
Rozpatrujemy wszystkie trapezy równoramienne, w które można wpisać okrąg, i w których suma długości dłuższej podstawy i średnicy okręgu wpisanego jest równa 6. Wyznacz wymiary tego spośród tych trapezów, który ma najmniejszy obwód. Oblicz ten obwód.
Rozwiązanie
Szkicujemy opisaną sytuację.
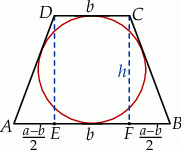
Jeżeli oznaczymy długości podstaw trapezu przez 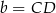 i
i 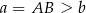 , to z założenia
, to z założenia 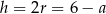 .
.
Trapez jest opisany na okręgu, więc
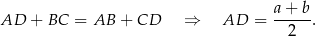
Obliczmy długość  krótszej podstawy trapezu – patrzymy na trójkąt prostokątny
krótszej podstawy trapezu – patrzymy na trójkąt prostokątny  .
.
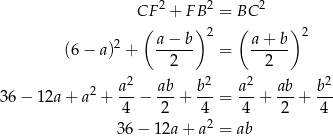
Zatem 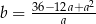 i obwód trapezu jest równy
i obwód trapezu jest równy
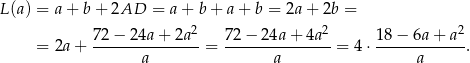
Dziedziną tej funkcji jest przedział 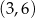 (bo
(bo 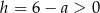 i
i 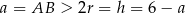 ). Liczymy pochodną funkcji
). Liczymy pochodną funkcji
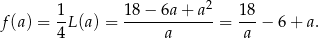
Jest ona równa
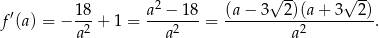
Widać teraz, że pochodna jest ujemna na przedziale 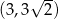 i dodatnia na przedziale
i dodatnia na przedziale 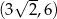 . To oznacza, że funkcja
. To oznacza, że funkcja 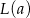 maleje na przedziale
maleje na przedziale 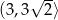 i rośnie na przedziale
i rośnie na przedziale 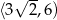 . Najmniejszy obwód trapezu otrzymamy więc dla
. Najmniejszy obwód trapezu otrzymamy więc dla 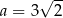 . Wtedy
. Wtedy
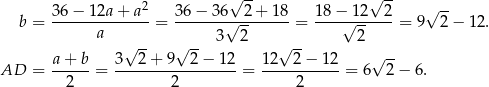
Obwód jest wtedy równy
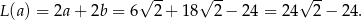
Odpowiedź: Podstawy: 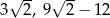 , ramię:
, ramię: 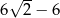 , obwód:
, obwód: 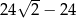 .
.

