/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema/Najmniejsza długość

Zadanie nr 9822312

Dodaj do ulubionych
Dodaj do rozwiązanych

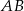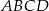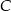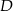Dany jest równoramienny trójkąt prostokątny, którego przeciwprostokątna ma długość 2. Bok AB prostokąta ABCD zawiera się w przeciwprostokątnej tego trójkąta, zaś punkty C i D należą do przyprostokątnych. Oblicz długości boków prostokąta 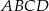ABCD wiedząc, że kwadrat długości jego przekątnej 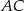AC ma wartość najmniejszą z możliwych.

Rozwiązanie

Zaczynamy od rysunku.

PIC

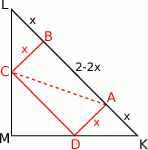
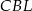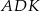Zauważmy, że trójkąty CBL i ADK są oba prostokątne i każdy z nich ma wspólny kąt z wyjściowym trójkątem 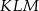KLM , czyli oba są prostokątne równoramienne. W takim razie

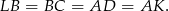
LB = BC = AD = AK .

Oznaczmy długość tego odcinka przez x . Wtedy x ∈ (0,1) i

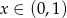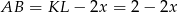
AB = KL − 2x = 2− 2x

i stosując twierdzenie Pitagorasa w trójkącie 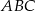ABC mamy

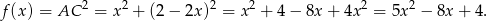
f(x) = AC 2 = x2 + (2 − 2x)2 = x 2 + 4 − 8x + 4x2 = 5x 2 − 8x + 4 .

Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość przyjmuje ona w wierzchołku, czyli dla

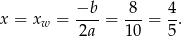
−b-- 8-- 4- x = xw = 2a = 10 = 5.

Zatem długości boków prostokąta są równe 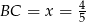BC = x = 45 i

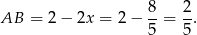
8 2 AB = 2 − 2x = 2− --= --. 5 5

 
Odpowiedź: 45, 25

Wersja PDF